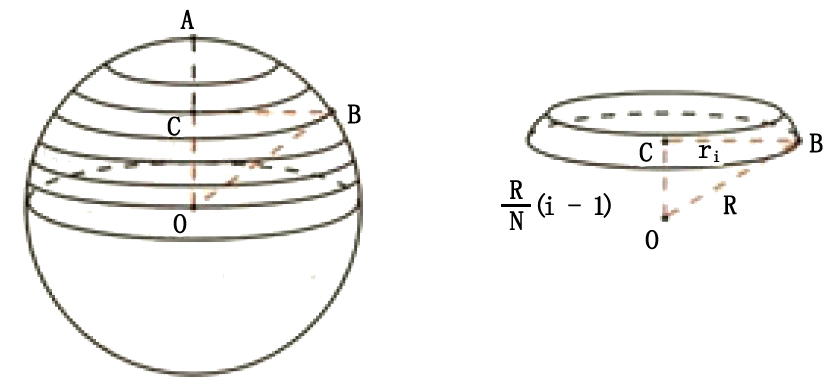
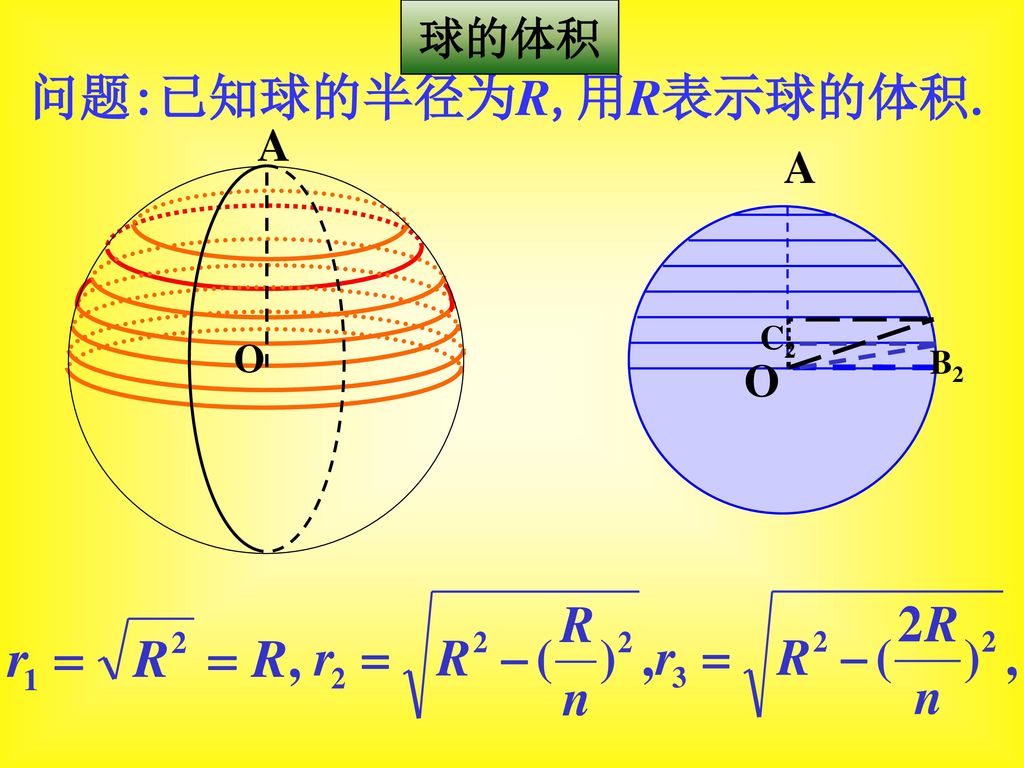
圆球表面积公式的推导圆球体积公式的推导过程
目次 Ⅰ 球欠と球冠の定義 言葉としてはあまり聞いたことのない「球欠」と「球冠」。 まずは言葉の意味を確認して球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半
球体 表面積 体積 公式
球体 表面積 体積 公式- せっかくなので、2次元、3次元、4次元、5次元の球の体積をこの公式を使って求めてみようと思います。 と言っても、 n n に整数を代入していくだけです。 2次元の時 (n = 2 n = 2 ):V 2 = 2π1 2Γ(1) Rn V 2 = 2 π 1 2 Γ ( 1) R n 3次元の時 (n = 3 n = 3 ):V 3 = 2π3/2 3Γ(3/2) R3 「球の体積の公式は丸暗記しなさい」 と言われている人も多いかと思います。 数学では「公式を丸暗記」というのはタブーに近いですが、今回はある意味しかたありません。 まずはこの公式をしっかりと覚えましょう! 公式の覚え方 それでは球体積公式を確実に覚えるためのコツを2

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
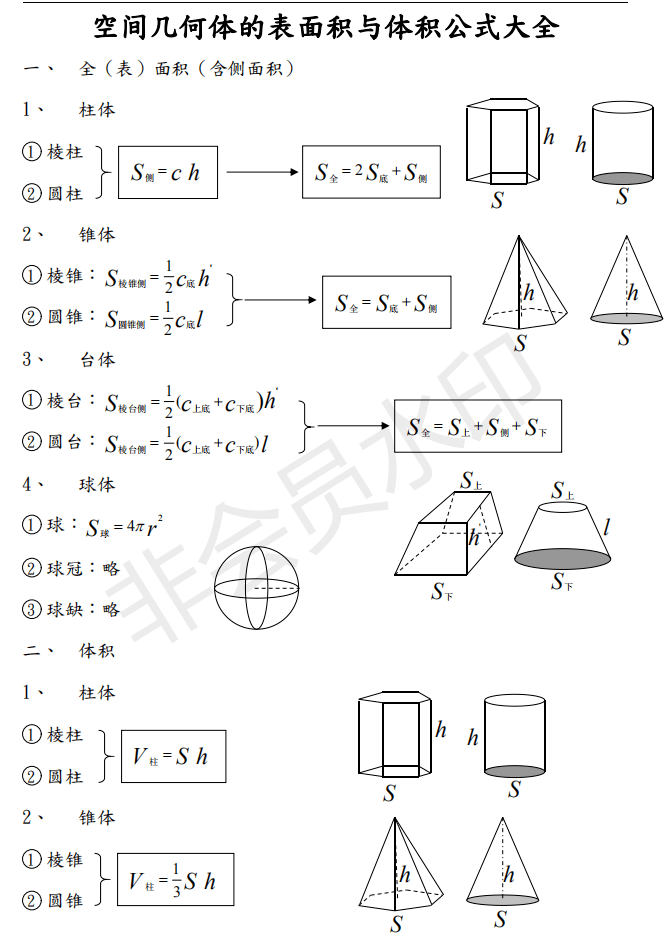
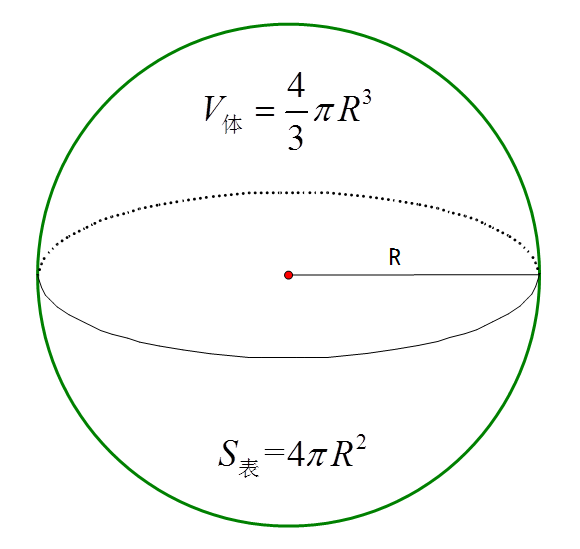
球の体積と表面積の公式 半径 r r r の球の表面積は S = 4 π r 2 , S=4\pi r^2,\ S = 4 π r 2 , 球の体積は V = 4 3 π r 3 V=\dfrac{4}{3}\pi r^3 V = 3 4 π r 3 である。 体積と表面積の公式を書き出し、\(r\)(半径)の値を当てはめて計算しましょう。 解答 球の体積 \(\displaystyle V = \frac{4}{3} \pi r^3\)表面積から半径を求める方法 表面積から半径を求める場合は、表面積から4と円周率を割り、その平方根を求めることで算出できます。公式で言うと、表面積を求める公式が S=2πr 2 なので、半径(r)を求める場合は、 r= S/4π となります。
微分 積分 球 円 体積 表面積 半径rの球の体積の公式は 4/3×pi×r×r×r(piは円周率) この式を変数rの関数としてrで微分すると 4×pi×r×r となり、 これは、言わずもがな、球の表面積の公式となります。 つまり、球の体積と表面積は、互いに微分積分の関係に体積や面積を求めるとき、 公式が通用しないとき は 『 部分 』+『 部分 』 『 全体 』-『 部分 』 を利用することはよくあります。 これはその典型です。 表面積は簡単には求まりませんが、部分部分は難しくはありません。 まずは半球の表面部分、壮大 球体 の 体積 の 求め 方 公式 球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 4/3πr³ になるよ。 つまり、 3分の4 × 円周率
球体 表面積 体積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
球体の表面積は、球の半径をr、面積をSとすると、「S=4πr2」 球体積の公式は「V=4─3πr3」 続きを読む 数学 算数 ・ 147 閲覧楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは( @t_kun_kamakiri )。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知り





0 件のコメント:
コメントを投稿